状态机和KMP算法
前言
字符串的匹配是编写程序的时候经常遇到的一个问题,也是计算机处理的基础问题之一。最简单的方法是循环字符串,一位一位地进行匹配,也可以使用正则表达式。今天本文讨论用状态机的模型如何理解和解决字符串匹配的问题。
状态机 FSM
状态机全称有限状态机(英语:finite-state machine,缩写:FSM)又称有限状态自动机(英语:finite-state automation,缩写:FSA),简称状态机,是表示有限个状态以及在这些状态之间的转移和动作等行为的数学计算模型。我个人的理解是我们的某一类型的问题在解决过程中能够抽象出有限个不同的状态,不同的问题只是问题解决过程中状态的转移过程不同,当我们将状态和状态之间的关系抽象出来,那么这一类问题我们全部能用一套逻辑来解决。每一个状态机应该能够接受相同的输出,每一个状态机都应该知道自己的下一个状态是什么(输出只依赖于当前状态,和输入无关的称为 moore 机,输出依赖于输出和当前状态的称为 mealy 机)。用 JavaScript 模拟状态机的模型大概如下面的形式。
function fsm_start(input) {
//当前状态机的逻辑
return next_fsm;//返回下一个状态函数
}
let state = fsm_start//设置初始状态
while (condition) {
state = state(input)//执行当前状态机函数,并将
}
状态机的字符串匹配
其实我们在编程的过程中其实一直和状态打交道,比如 if/else,switch/case等,有时候当我们面对一些比较复杂的问题的时候如果能够用有限状态机来描述,那么问题的逻辑可能更清晰。代码结构的可读性也更强。
比如字符串的匹配问题,当我们想要知道某个字符串中是否包含另一个字符串时,状态机就能够帮我们解决问题。比如我们要寻找一个字符串中是否有 abcdef 这串字符,如果使用状态机模型,我们可以这样实现:
function match(string) {
let foundA = foundB = foundC = foundD = foundE = false;
for (let c of string) {
if (c === 'a') {
foundA = true;
} else if (foundA && c === 'b') {
foundB = true;
} else if (foundB && c === 'c') {
foundC = true;
} else if (foundC && c === 'd') {
foundD = true;
} else if (foundD && c === 'e') {
foundE = true;
} else if (foundE && c === 'f') {
return true
}
}
return false;
}
console.log(match('abcdeabcdef'))//true
但是如果我们想要匹配的字符串时 abcabx 这种有重复部分的时候我们就没法用上面那种方法了,因为当我们匹配到 x 这一位的时候有可能是 c 我们需要回到检测到 c 的状态,这种情况用上面的方法就没法实现,因为 if/else 结构是没法跳转到某一步的。在不用状态机的情况下我们可以用下面的“暴力”方法实现,用 i 和 j 分别表示字符串和 pattern 当前正在匹配的字符的下标,匹配成功则都 +1,否则 i = i - j +1,j = 0。循环继续的条件是字符串还没匹配完,并且也没有成功匹配出 pattern。大概过程如下图。
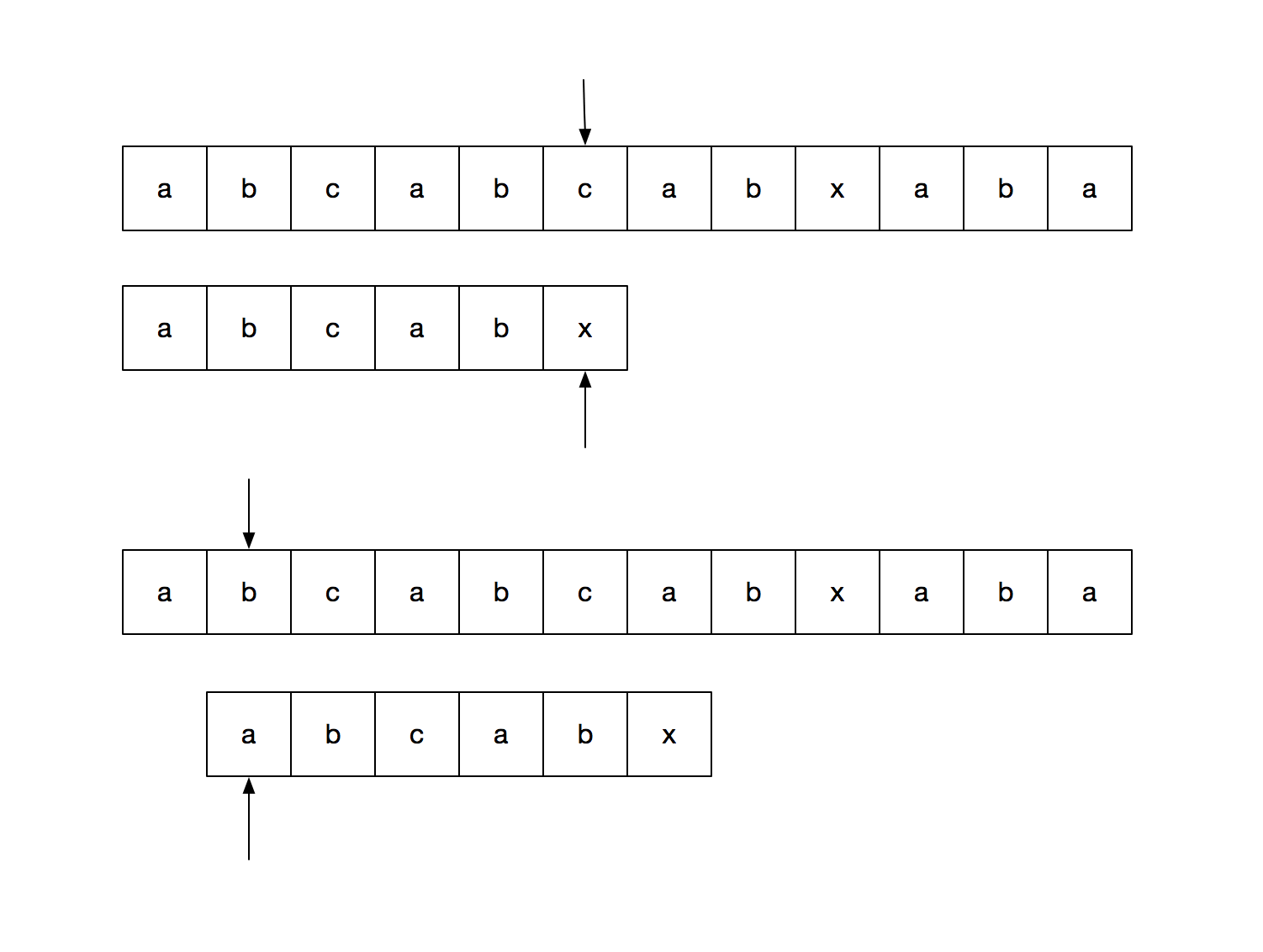
function match(string, pattern) {
let i = j = 0;
for (; i < string.length && j < pattern.length; i++) {
if (string[i] === pattern[j]) {
j++;
} else {
i -= j;
j = 0;
}
}
if (j === pattern.length) {
let s_index = i - pattern.length;
return [s_index, string.slice(s_index, s_index + pattern.length)];
} else {
return 'failed'
}
}
console.log(...match('abababababcabcabxababab', 'abcabx'))
用上面的方式我们可以对任意 pattern 进行字符串的匹配。但有个问题是当匹配失败的时候我们是将 i 前进一位,然后对 pattern 从头进行匹配,对一些有重复部分的 pattern 显然是没有效率的。比如 abcabx,当我们匹配到 abcabc 的时候我们没必要从 bcabc 从头匹配,只需匹配第二个 abc 后面是不是 abx 就可以了。而如果使用状态机模型,则可以利用状态的跳转来实现这样的目的。
function match(string) {
let state = start;
for (let c of string) {
state = state(c);
}
return state === end;
}
function start(c) {
if (c === 'a') {
return foundA;
} else {
return start;
}
}
function foundA(c) {
if (c === 'b') {
return foundB;
} else {
return start(c);
}
}
function foundB(c) {
if (c === 'c') {
return foundC;
} else {
return start(c);
}
}
function foundC(c) {
if (c === 'a') {
return foundA2;
} else {
return start(c);
}
}
function foundA2(c) {
if (c === 'b') {
return foundB2;
} else {
return start(c);
}
}
function foundB2(c) {
if (c === 'x') {
return end;
} else {
return foundB(c);//跳转到找到第一个b的状态
}
}
function end() {
return end;
}
console.log(match('ababaabcabcabxab'))//true
用状态机模型的方式实现,代码结构也很清晰,每一个状态直接是没有关系的,我们可以通过控制状态的跳转来控制流程,提高匹配的效率。但是这样的实现方式显然也不好,每次出现一个新的 pattern 我们都要重新写代码,并没有将状态机的逻辑完全抽象出来。
KMP 算法
KMP算法的主要思想是提前判断如何重新开始查找,而这种判断只取决于模式字符串本身。—— 《算法4》
在匹配字符串这个问题上,最重要的就是当一个字符匹配失败的时候,我们怎么进行下面的匹配才是最高效的。比如上面的非状态机的实现方法,当我们匹配失败的时候,我们已经匹配成功了 [0, j - 1] 位了,此时我们将 i 回退到未匹配状态并右移一位再从 j = 0 开始匹配,这显然是非常低效的。比如 abcabx 这样的 pattern,当我们在 x 这一位匹配失败的时候,我们并不一定需要全部重新匹配,因为如果我们当前这一位是 c 的话我们可以优化我们的匹配过程,如下图。
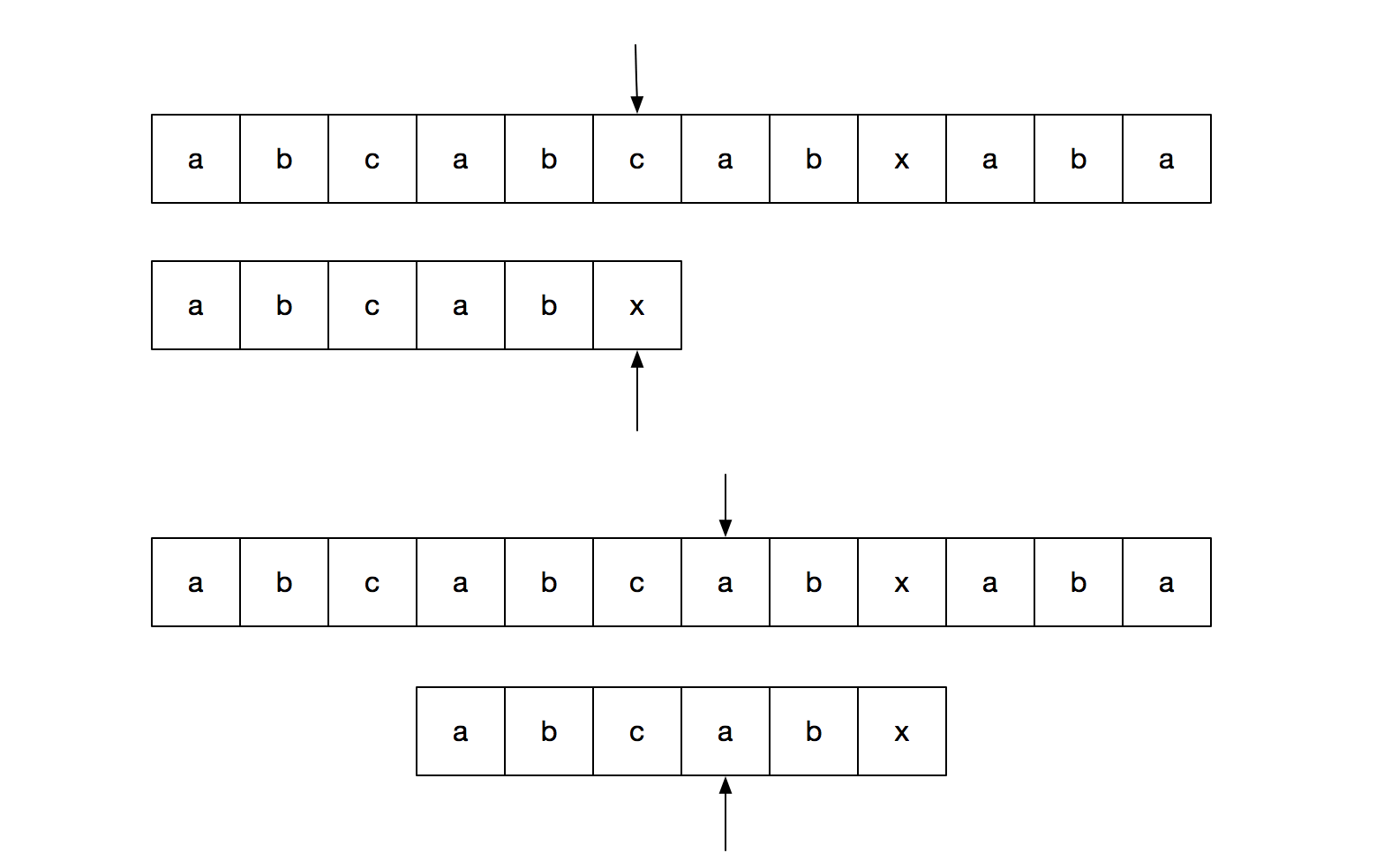
如果我们能找到 pattern 的规律就能够很好地优化我们的过程,kmp 算法正是一个很好字符串匹配的算法。kmp 算法有两种实现方式,一种是基于确定有限状态机的 DFM(deterministic finite-state automaton),另一种是基于部分匹配表 PMT(Partial Match Table) 的。我个人觉得 PMT 的思路更容易理解一点,但是 DFM 则是一种更”优雅“的方式。
DFM
在谷歌上搜索 DFM 的中文结果很少,大部分的 KMP 算法的文章都是讲解 PMT 中的 next 数组的含义,通过状态机来讲解这个算法的非常少,而且质量也不是很高。大部分的 DFM 文章都来源于 《算法》第四版 中的 5.3 章节 Substring Search 中的 Knuth-Morris-Pratt substring search,以及作者 Robert Sedgewick 对该算法的讲解视频(视频地址贴在这里)。我最后也是直接看原文和视频来理解的(虽然英文很烂,硬着头皮看,不过视频还好,没有什么听力难点,学好英语对程序员太重要了),这里整理一下我的理解。我认为重点是要理解状态转移之间的关系,这是 DFM 的核心。
首先贴上《算法》中的对字符串 ABABAC 作为 pattern 的状态机图示。
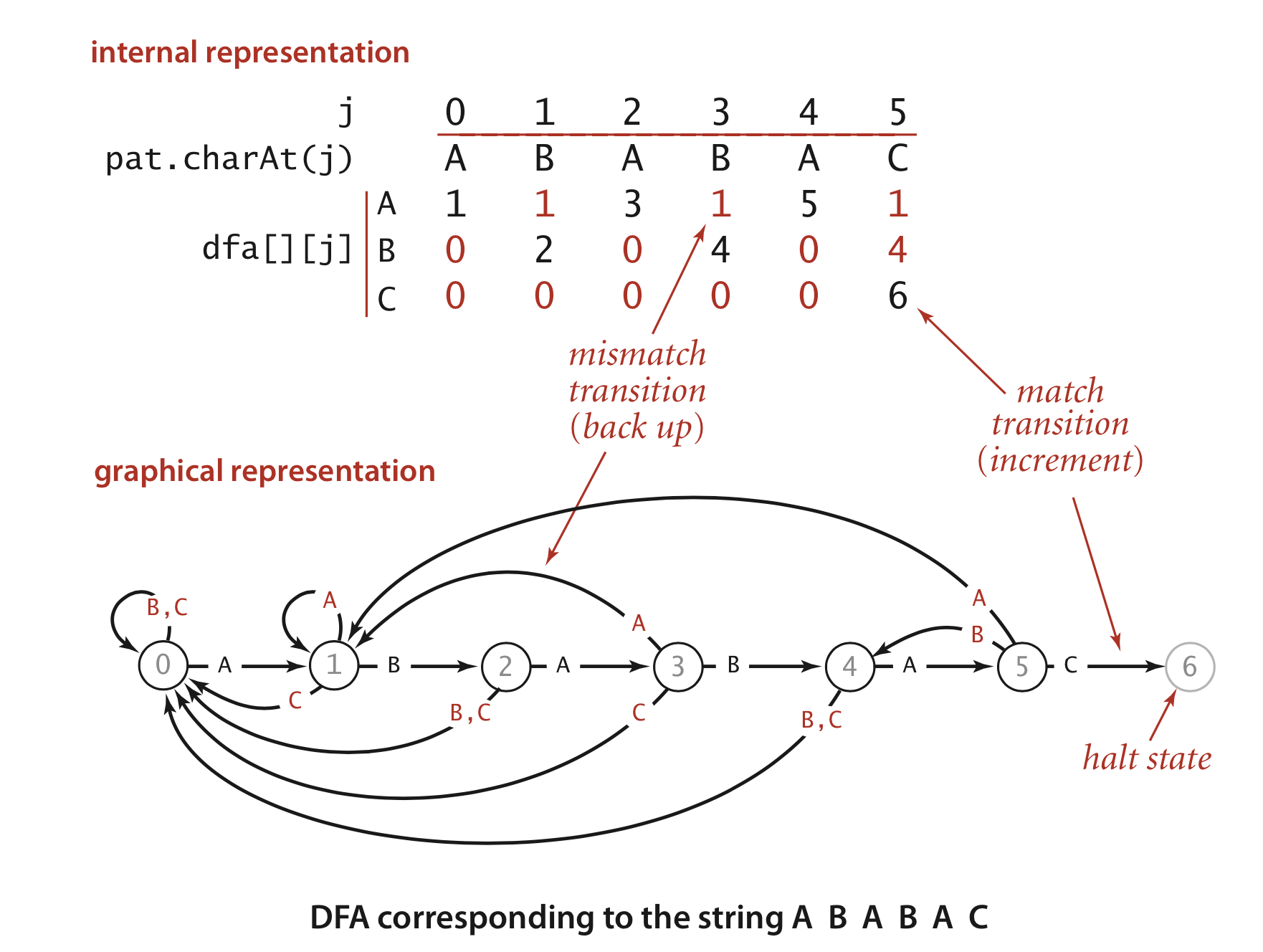
对这两个图做一个简单的解释,上方的是一个矩阵,下方是一个图表,他们表达的是同一个有限状态机,只是形式不同。这两张图表达的就是 ABABAC 进行匹配的状态机。所有的数字表示的都是状态,而这个状态数字可以理解成当前已经成功匹配了几个字符,比如状态 4 表示已经成功匹配到了 ABAB 才进入状态 4。下方图表的箭头则表示状态的转移,注意每个箭头上都有一个字母,表示这个转移是因为这个字母的输入。以状态 3 为例,我们此时已经成功匹配到了 ABA 三个字符,下面我们接受的输入有三种可能 A B C,当接收 B 时,我们成功匹配进入状态 4,当接收 A 时,我们回到了状态 1,当我们接收 C 时回到状态 0。我们的状态机接收两个参数,一个是当前状态,一个是输入,得到的结果就是应该转移的状态。在矩阵图中,j 是当前所处的状态,pat.charAt(j) 表示 pattern 在当前要匹配的字符,纵向的 dfa[][j] 则表示输入,中间的矩阵表示要转移到的状态,比如矩阵中位置 [0,0] 的 1 表示,在状态 0 接收输入 A,状态转移到 1。
这里需要注意,我们的状态机只和
pattern有关,就是不管我们要进行匹配的字符串是什么,只要我们的pattern不变,状态机就不变,举个例子就是不管待匹配的字符串是ababababaaacaba还是abafabafagaba,只要pattern是ABABAC,状态机就不变,所以在分析状态机的时候我们只需要分析在pattern中出现的字符。
我们将待匹配的字符串叫做 string,把要匹配的子串成为 pattern
这里的状态是我们自己分析的,但是要写成程序我们必须抽象出一个所有 pattern 的状态机规律。我们想一想我们是如何得到状态转移 (state transition) 的结果的。以状态 5 为例,当我们在状态 5 匹配失败 (mismatch) 的时候,我们如何确定我们要转移到哪个状态呢。这里可以借助上面的暴力解法来理解,当我们在状态 5 匹配失败的时候,我们已经成功匹配了 ABABA,此时按照暴力解法,我们应该是从 BABA 开始重新匹配。我们可以确定的是 BABA 也是 pattern 的子串,所以其实我们只要搞清楚 BABA 在状态机中执行后会到什么状态,这个状态被称为 restart state。也就是说,当我们在 j 处匹配失败,我们只要知道知道 1 ~ (j-1) 这个子串在状态机中运行后的状态,这个状态就是状态 j 的重启状态 restart state,所以 j 处的某个输入 c 匹配失败了,我们获得其状态转移的方法就是将这个输入 c 交给重启状态即可。而 j 的 restart state 也有自己的 restart state,我们只要找到重启状态之间的关系就可以用迭代来解决这个问题,因为状态 0 没有 restart 状态,而状态 1 的 restart state 肯定是 0(状态 1 去掉首位就是个空字符串),有了初始状态和迭代规律,我们并不需要真的把 BABA 放到状态机中运行然后记录结果,只是帮助我们理解这个算法。
我们用一个变量 X 表示当前状态下匹配失败要跳转到的状态。我们上面说过,当状态 5 匹配失败时,我们实际上是将 ABABA 去掉首位变成 BABA 进入状态机运算得到的结果作为状态 5 的 X,也就是说当我们在状态 j 匹配失败时,我们是将 pattern 中已经匹配成功的 pattern[0] - pattern[j - 1],去掉首位,也就是 pattern[1] - pattern[j - 1] 放入状态机中运算,得到的结果作为 X。我们还是以 ABABAC 为例,分析一下各个状态的 X。
语言能力不太好,下面的表述可能不太清晰。主要有三个概念:X是当前状态的restart state,目标字符是当前状态能匹配成功的字符,还有一个就是求X需要的当前状态已匹配的字符串(去掉首位,比如上面的 BABA)
- 状态
0,目标字符A,一个字符都没有匹配成功,不考虑。 - 状态
1,目标字符B,匹配成功A去掉首位为"",放入状态机中运算结果为0,X为0。 - 状态
2,目标字符A,匹配成功AB去掉首位为B,放入状态机中运算结果为0,X为0。 - 状态
3,目标字符B,匹配成功ABA去掉首位为BA, 放入状态机中运算结果为1,X为1。 - 状态
4,目标字符A,匹配成功ABAB去掉首位为BAB,放入状态机中运算结果为2,X为2。 - 状态
5,目标字符C,匹配成功ABABA去掉首位为BABA,放入状态机中运算结果为3,X为3。
我观察一下可以发现,去掉没意义的状态 0,剩下的五个状态,求 X 所用的字符串分别是 "",B,BA,BAB,BABA,而目标字符分别是 B,A,B,A,C,状态 2 的 X 值就是状态 1 的 X 对应状态输入状态 2的目标字符 A 得到的状态。注意这里的X代表的也是一个状态
可能有点绕,不是很好表述,状态 5 的 X 就是 BABA 在状态机中的运算结果,状态 4 的 X 就是 BAB 在状态机中的运算结果,BABA 的运算结果就是 BAB 的运算结果再输入一个 A,而这个 A 就是状态 4 的目标字符。也就是说我们知道状态 4 的 X 就已经能求得状态 5 的 X,以此类推我们从状态 1 就能求到之后所有状态的 X,而状态 1 的 X 为 0。
restart state 我认为两个作用:
1. j 和 j-1 状态的 restart state 有明确的迭代关系,我们可以利用状态 1 的 restart state 为 0和迭代关系两个信息求出所有状态的 restart state。
2. 当前状态的不匹配输入是交给 restart state 处理的(如果这个输入给 restart state 也不匹配,那么就会找 restart state 的 restart state也就是说,我们某个状态的不匹配输入 c 的结果是从其 restart state 上复制的。
根据这两条规律,我们只要有状态 0 的所有输入结果,我们就可以得到所有状态的状态跳转矩阵。具体到代码上,我们可以创建一个二维数组 dfa[][],我们初始化 dfa[0][] 的所有项,然后根据上面两条规律,可以生成整个 dfa 矩阵,我们的问题也就迎刃而解。
《算法》第四版中有两张图可以来辅助理解。
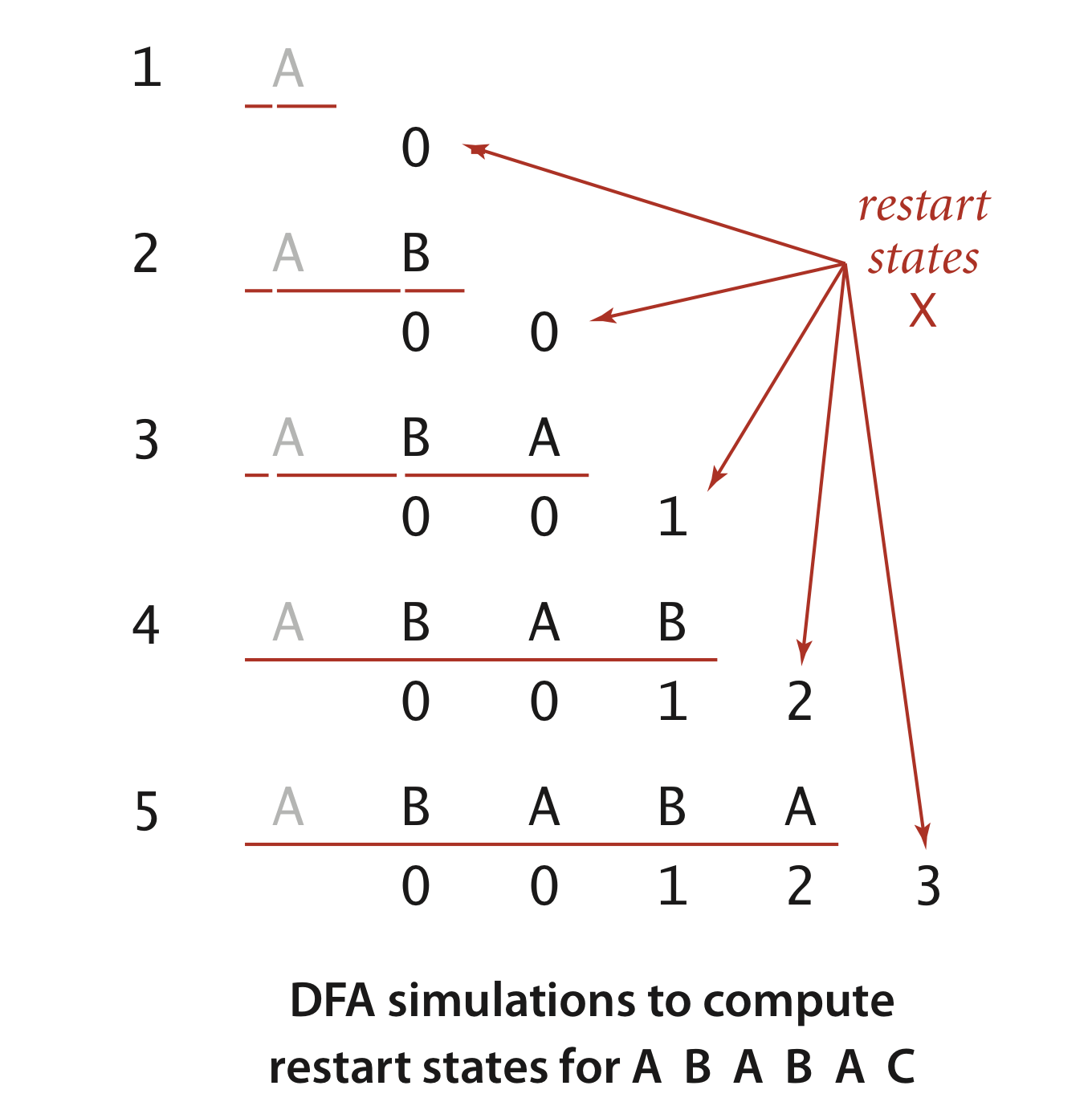

下面就是具体代码,我们可以分成两个部分,一个部分是检索子字符串,另一部分是管理状态机。第一部分的代码非常简单,循环字符串,将字符交给状态机,当字符循环完毕没匹配成功则返回 false,若匹配成功则返回 success。第二部分则是生成对应 pattern 的状态机。
function match(s, p) {
let M = p.length,
N = s.length,
i = 0,
j = 0,
dfa = KMP(p);
for (; i < N && j < M; i++) j = dfa[j][s.charCodeAt(i)];
if (j === M) return 'match success at index of ' + (i - M);
return 'false';
}
function KMP(p) {
let X = 0,
R = 256,
M = p.length,
dfa = new Array(M);
for (let i = 0; i < dfa.length; i++) dfa[i] = new Array(R); //创建长度为dfa.length的数组,每一项为一个对象
//初始化dfa[0],即初始的X状态,后面的状态要用这一状态来复制
for (let i = 0; i < R; i++) dfa[0][i] = 0;
dfa[0][p.charCodeAt(0)] = 1; //状态0时匹配到第一位总是进入状态1
//生成后面的状态机
for (let j = 1; j < M; j++) {
for (let c = 0; c < R; c++) dfa[j][c] = dfa[X][c] //设置状态j的匹配失败项,从状态X复制
dfa[j][p.charCodeAt(j)] = j + 1;//设置匹配成功项
X = dfa[X][p.charCodeAt(j)] //计算下一状态的 X
}
return dfa;
}
console.log(match('asdfasdfsafabababafabababacasdf', 'ababac'));
这里的代码使用 javascript 写的,所以 KMP 中我们需要手动初始化状态 0(也就是默认的 X)的状态跳转。《算法》中的代码使 Java,所以整形数组的项的默认值是 0,不需要处理。 javascript 中,new Array() 方法创建的固定长度的数组其实只是一个确定了 length 属性的数组对象,里面并没有任何元素(不要理解成都是 undefined)。
还有一点就是算法中是用 charAt,也就是 javascript 中的 charCodeAt 方法来设置状态机的输入,每个状态对应 256 种输入,也就是扩展 ASCII 码的全部字符数,这样做的好处是我们完全不需要考虑 match 函数中的输入字符(只要在扩展 ASCII 范围内)。不过这样创建的二维数组特别大,我认为可以先对 pattern 进行一个处理,取出 pattern 中所有的不重复的字符放入对象,只要匹配的字符不在这个对象中,直接将 j 设置为 0。具体代码如下。
function match(s, p) {
let M = p.length,
N = s.length,
i = 0,
j = 0,
o = {},
dfa = KMP(p);
//生成pattern中不重复元素的对象
for (let t of p) {
if (!o[t]) o[t] = t;
}
for (; i < N && j < M; i++) {
j = !!o[s[i]] ? dfa[j][s[i]] : 0;
}
if (j === M) return 'match success at index of ' + (i - M);
return 'false';
}
function KMP(p) {
let X = 0,
R = 256,
M = p.length,
o = {},
dfa = new Array(M);
//生成pattern中不重复元素的对象
for (let t of p) {
if (!o[t]) o[t] = t;
}
for (let i = 0; i < dfa.length; i++) dfa[i] = {...o}; //创建长度为dfa.length的数组,每一项为一个对象
//初始化dfa[0],即初始的X状态,后面的状态要用这一状态来复制
for (let key in dfa[0]) {
dfa[0][key] = 0;
}
dfa[0][p[0]] = 1; //状态0时匹配到第一位总是进入状态1
//生成后面的状态机
for (let j = 1; j < M; j++) {
for (let c in o) dfa[j][c] = dfa[X][c] //设置状态j的匹配失败项,从状态X复制
dfa[j][p[j]] = j + 1;//设置匹配成功项
X = dfa[X][p[j]] //计算下一状态的 X
}
console.log(dfa)
return dfa;
}
console.log(match('asdfasdfsafabababafabababacasdf', 'ababac'));
//[
// { a: 1, b: 0, c: 0 },
// { a: 1, b: 2, c: 0 },
// { a: 3, b: 0, c: 0 },
// { a: 1, b: 4, c: 0 },
// { a: 5, b: 0, c: 0 },
// { a: 1, b: 4, c: 6 }
//]
//match success at index of 21
状态机的运用让我们在搜索的效率上得到了很大的提高,但是我们需要额外维护一个状态机,也是用空间换时间。暴力解法的时间复杂度最坏情况是 O(m*n),DFM 的解法的时间复杂度则为 O(n).
PTM 部分匹配表
在搜索引擎上能找到的关于 KMP 算法的文章大部分都是 PTM 实现的,所以我也是最先看的 PTM 实现。相对于 DFM 的实现,PTM 的实现可能更简单粗暴一点,也更好理解。而且 PTM 的思维可能会影响你对 DFM 的理解。
PMT 叫做部分匹配表,其实就是把 DFM 中每个状态对应的 X 的值进行单独计算。在 DFM 中我们对 X 的理解是一个在匹配失败的时候跳转的状态,在 PTM 中对这个值的理解就是当前状态下的最长前后缀。
我们先来介绍前后缀的概念。对于一个字符串,包含该字符串的首位且不包含末位的子串就是这个字符串的前缀,而包含该字符串的末位且不包含首位的子串就是这个字符串的后缀。比如对于字符串 ababa ,他的前缀包括 a ab aba abab, 他的后缀包括 a ba aba abab。我们在 DFM 中找的 X 在 PTM 的理解中就是寻找最长的相同前后缀。比如 ababa 的最长相同前后缀就是 aba,长度为 3。我们在 DFM 中的 ABABAC 的 j 为 5 的情况下对应的 X 就是 3。这个原理其实也很简单,看下图。
在 DFM 中我们理解这张图是我们在 j 为 5 的状态匹配失败,此时我们将前面匹配成功的五位 ABABA 去掉首位再放到状态机中计算得到的输出作为 X。在 PTM 中其实就没有所谓的状态了,我们在当前这一位匹配失败了,就找出前面匹配成功的字符串 ABABA 中的最长前后缀,也就是 ABA。其实我们仔细思考一下,这两种方法其实并没有本质的区别,把 BABA 放到状态机中计算就是找最长前后缀,只不过 DFM 更巧妙一些,我们不需要真的去找最长的前后缀。可以说 DFM 的做法是着眼于各个状态的关系,用这个关系来解决问题;而 PTM 则更简单直接一点,我这个状态的问题就利用这个状态自己解决。
所以在 PTM 中我们可以得出 pattern 的各位对应的最长相同前后缀的长度,这个长度所形成的表就叫做部分匹配表。我们用两个 pattern 来看一下对应的 PTM 。第一个是 ababac,第二个是 abababca。
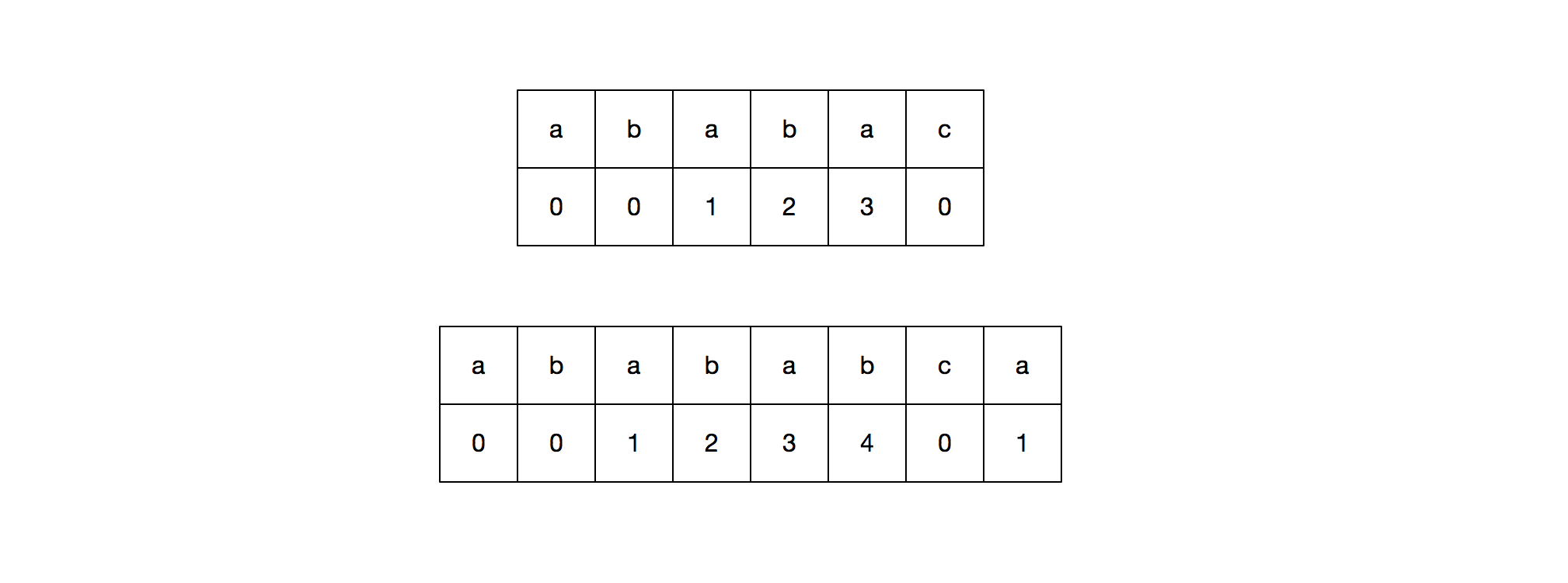
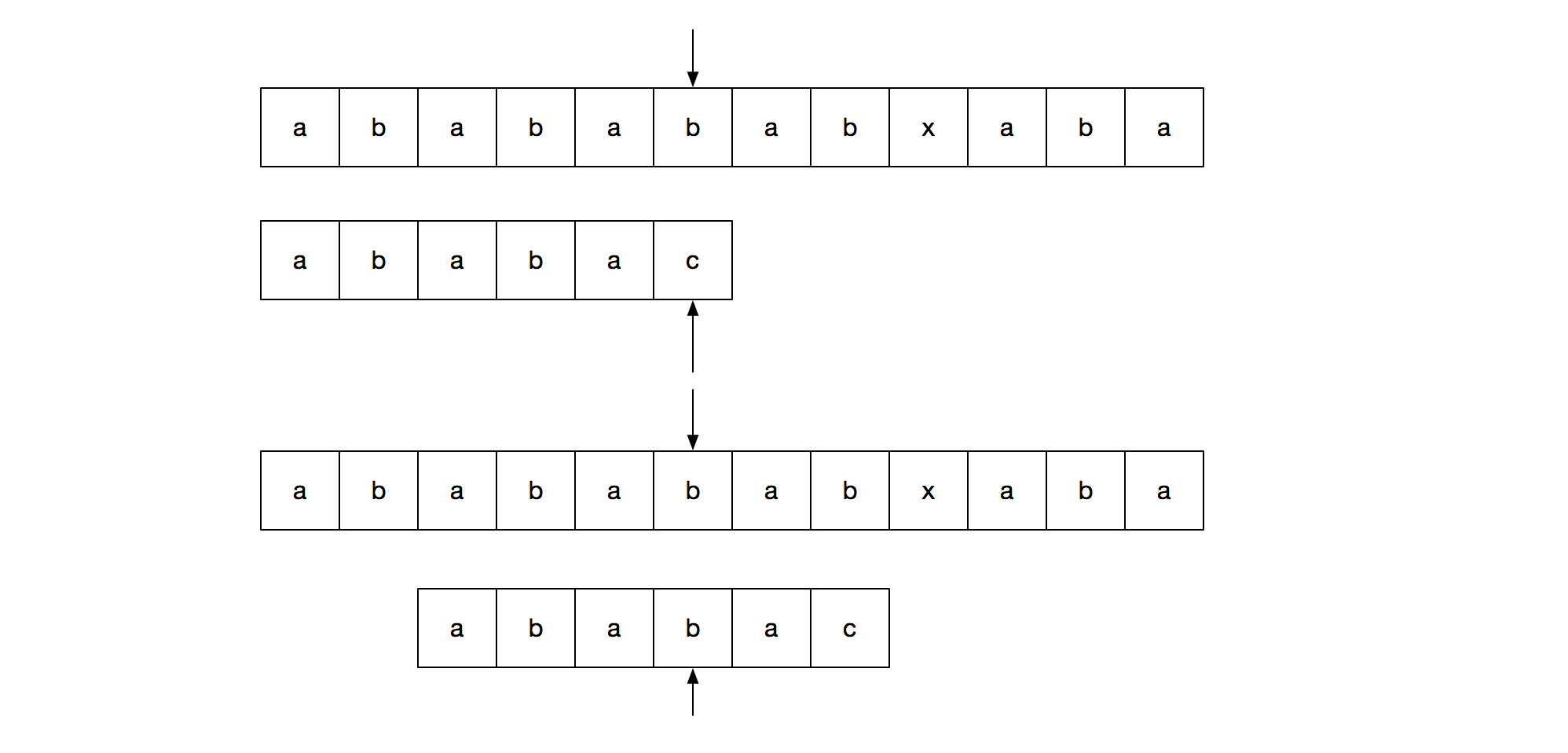
如何求这个 PTM 呢?其实 PTM 就是 pattern 自己和自己匹配然后得出的结果,因为我们在用 pattern 和字符串匹配的时候,匹配成功的组合必然就在 pattern 中,匹配失败的时候我们需要移动的也只是 pattern 的指针,所以 PTM 只和 pattern 相关。大概的逻辑是:从 pattern[1] 开始不断用 pattern 进行匹配,用两个指针分别指向两个 pattern 当前的位置(如下图),用一个数组 arr 储存 i 指针对应位的最长前后缀的长度。匹配成功则两个指针都右移,arr[i] = j(得到当前位置的最长前后缀);失败则 i 不动,j 赋值为 arr[j-1] 的值(在运行过程中就利用我们已经得到的结果);如果 j 为 0,则 arr[i] = 0 并且 i 向右移动一位。整个过程就是 DFM 中的某一位匹配失败时,用前面匹配成功的部分去掉第一位放进状态机匹配的详细过程。详细的过程和代码看下图
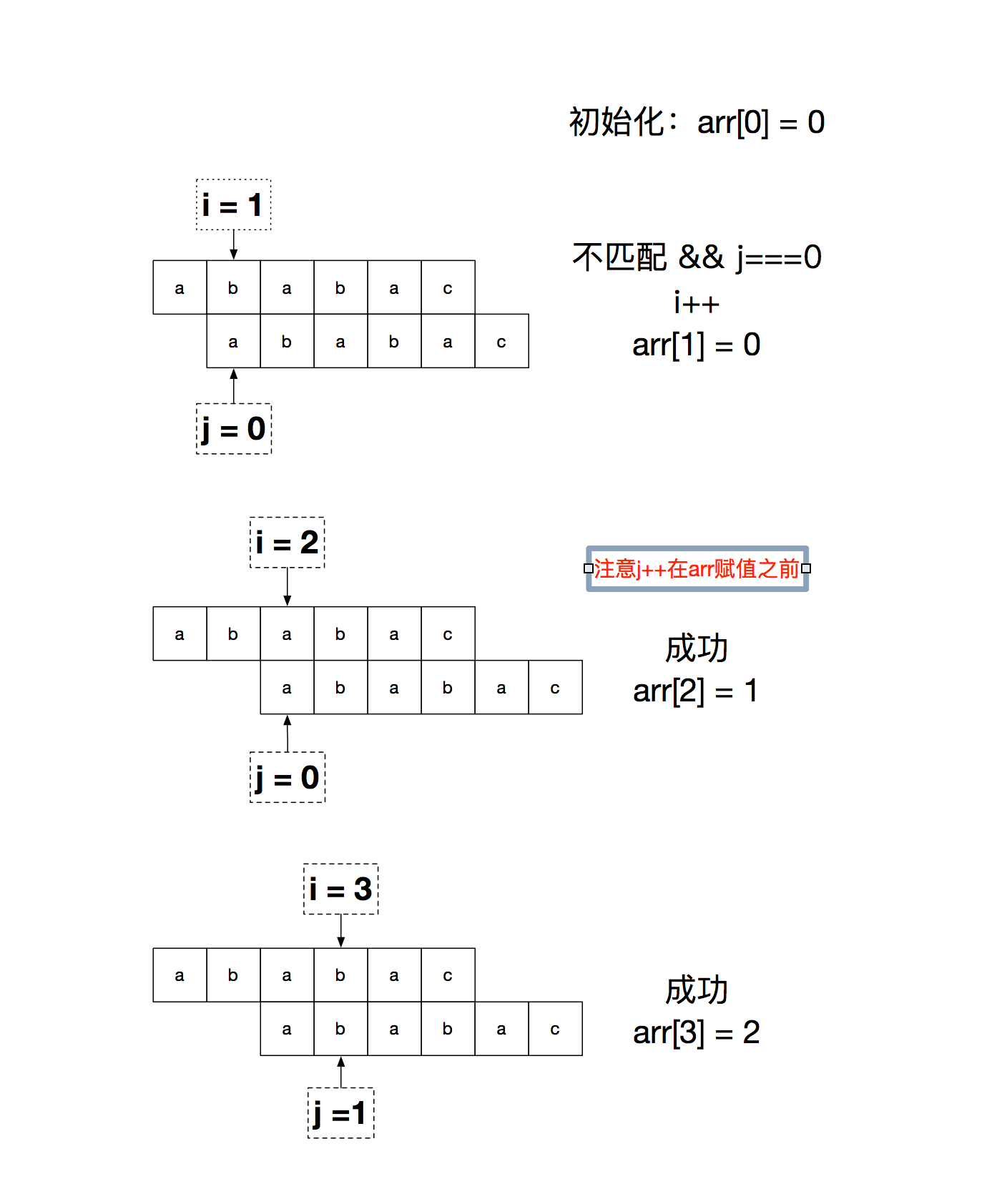
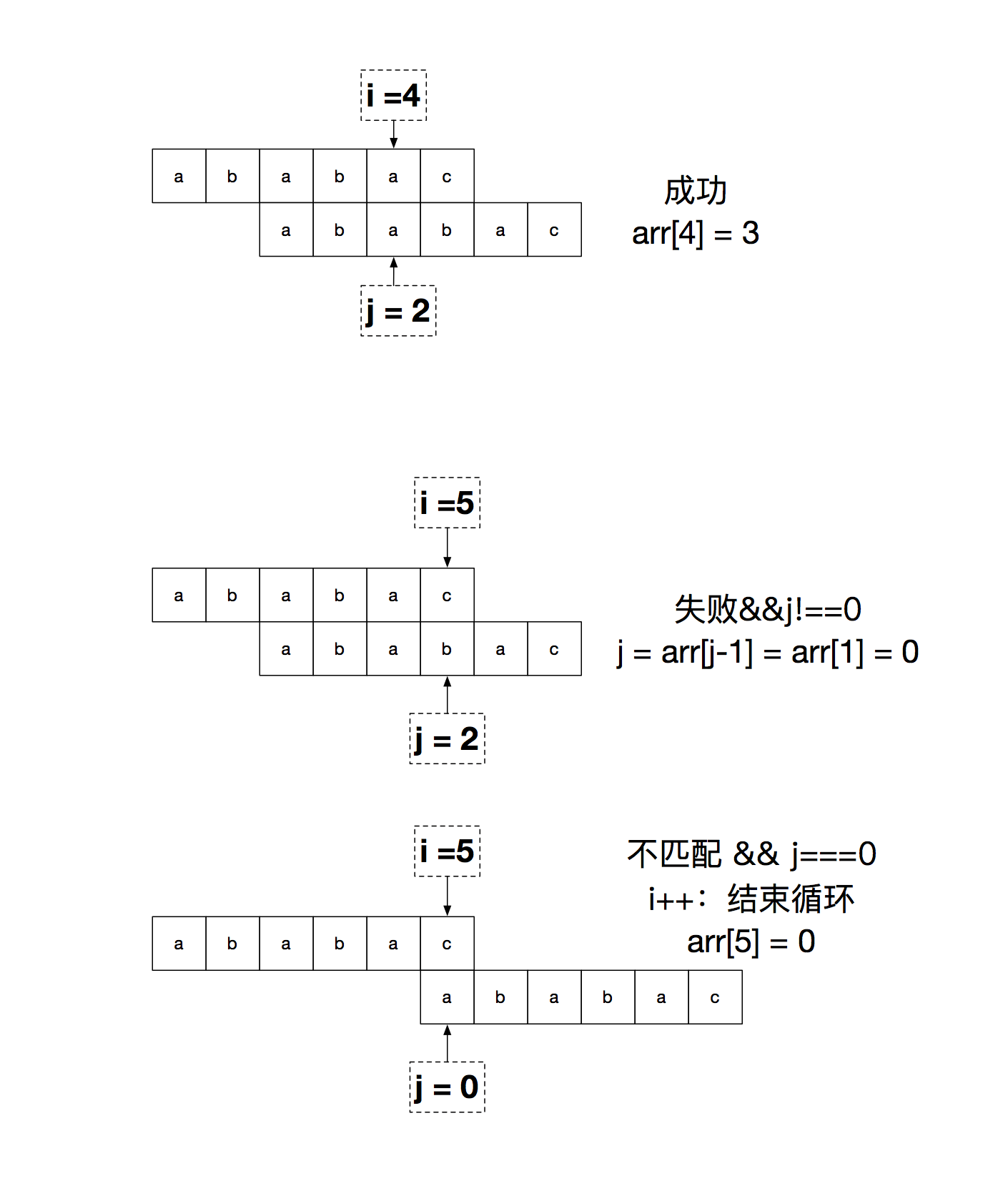
function PMT(p) {
let i = 1,//i和j错开
j = 0,
arr = [0];//第一位的最长前后缀为0
while (i < p.length) {
if (p[i] === p[j]) {
j++;
arr[i] = j;
i++;
} else if (j === 0){
arr[i] = 0;
i++;
} else {
j = arr[j - 1];//匹配失败的时候,j回到j-1位的最长前后缀的位置
}
}
return arr;
}
console.log(PMT('ababac'))
console.log(PMT('abababca'))
//[ 0, 0, 1, 2, 3, 0 ]
//[ 0, 0, 1, 2, 3, 4, 0, 1 ]
我们上面求得的这个 PTM 在实际编码中并不方便,我们上面的 i 指针实际上相当于我们在 i + 1 位匹配失败,求得前 1 ~ i 位的最长相同前后缀(即 DFM 中的把 1 ~ i 位放到状态机中执行),所以 i 位的 PTM 值其实是给 i + 1 位用的,基于这个原因,我们将 PTM 表向右移动一位,最左边补上一个 -1(单纯是为了编程方便),最右边的位舍去,得到如下的 next 表。
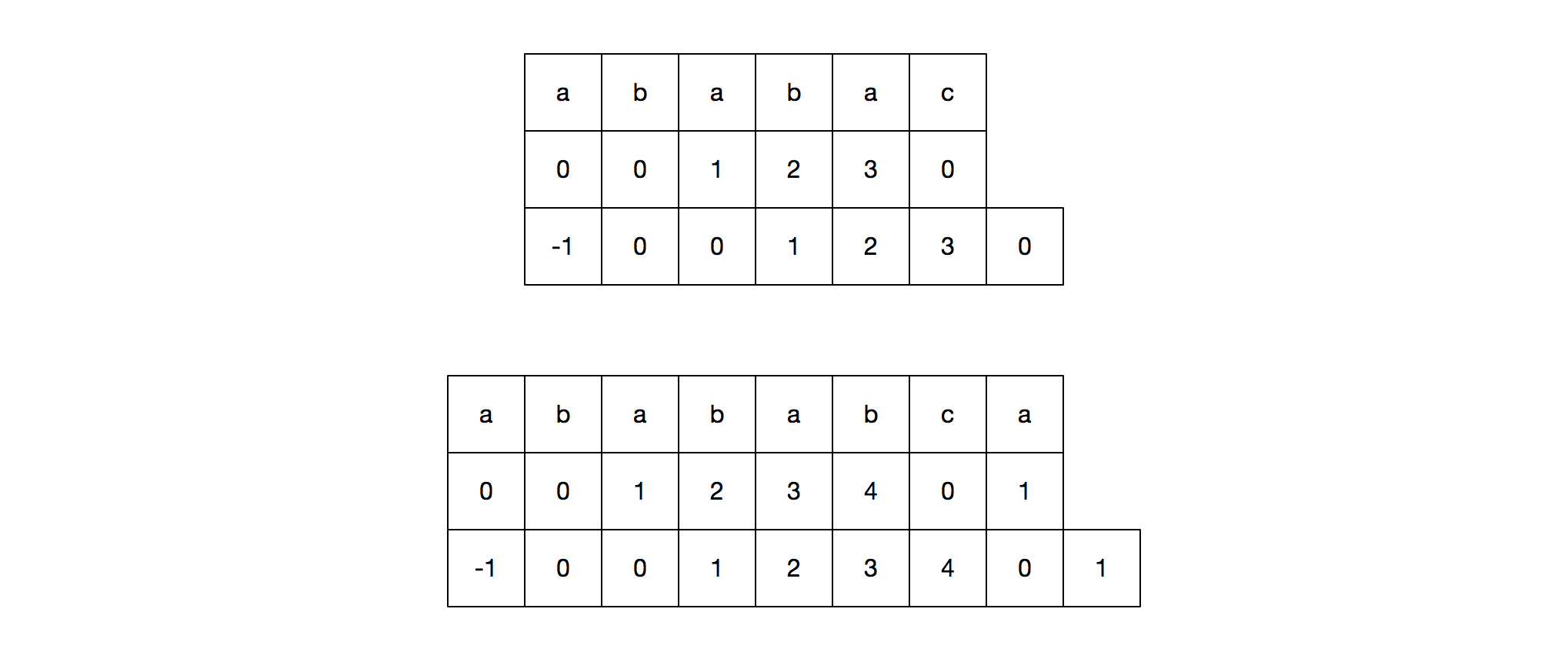
我们也可以直接求出 next 数组,代码如下。
function PTM2(p) {
let arr = [-1];
let i = 0, j = -1;
while (i < p.length)
{
if (j == -1 || p[i] == p[j])
{
++i;
++j;
arr[i] = j;
}
else
j = arr[j];
}
//arr.pop();
return arr;
}
console.log(PTM2('ababac'))
console.log(PTM2('abababca'))
//[ -1, 0, 0, 1, 2, 3, 0 ]
//[ -1, 0, 0, 1, 2, 3, 4, 0, 1 ]
我们可以看出我们设置 arr[0] 和 j 为 -1 的情况下,我们可以将 j 回到第一位和匹配成功两个状况合并,因为 j 回到第一位理论上只要移动 i,但当我们设置 j 为 -1 的时候,我们也需要 j++,这就和匹配成功的逻辑相同了,让我们的代码更简单更清晰。得到 next 数组之后剩下的就是写 match 函数,逻辑和 next 数组的逻辑基本相同。
function match(s, p) {
let i = 0,
j = 0,
arr = PMT(p);
while (i < s.length) {
if (j === -1 || s[i] === p[j]) {
if (j === arr.length - 1) return 'success';
i++;
j++;
} else {
j = arr[j];
}
}
return 'failed';
}
总结
我个人认为动态规划是有限状态机的一种特殊形态。DFM 的实现花了很长时间才领会,主要就是因 PTM 的想法有点先入为主的理解,他们的本质是一样的,但是 DFM 用状态之间的关系迭代直接避免了比较复杂的前后缀计算,我们只关心每个状态之间的关系,有一点动态规划中走楼梯问题的感觉。不过KMP 算法似乎也不是查找子串效率最高的方法,在 《算法》第四版中还有一个 Boyer–Moore 算法。



