原码,反码和补码
前言
以前在学习计算机科学导论的时候,仔细研究过原码,反码,补码之间的关系以及他们是用来解决什么问题产生的。今天在看 JavaScript 中的 Number 的时候想到这三个概念,用一篇文章来整理一下相关的知识。
机器数和真值
虽然我们有反码补码的概念,但是对于硬件来说,他们完全不明白这是什么。对于硬件来说,有 n 位存储单元,就有 $2^n$ 个状态,也就能表示 $2^n$ 个数。也就是说原码,反码和补码都是人为创造出来的概念,其目的就是用数学的方法来简化硬件的设计。比如我们规定了最高位为符号位,那么一个 8 位的存储单元可以用 10000001 来表示 -1,其中这个 10000001 就是机器数,而 -1 就是真值。
原码
计算机要进行计算就必须存储数值,最简单的方法就是用机器码作为我们的真值,比如一个 8 位的存储单元可以存储 00000000 ~ 11111111 共 256 种数字,真值从 0 ~ 255,但是这样设计显然意义不大,因为我们需要计算负数。为了引入负数,所以设计出了原码:用存储单元的第一位表示符号,1 位负,0 为正,后面的位表示真值的绝对值。同样以 8 位存储单元位例,在用原码的方式下我们依然可以表示 256 个数,从 11111111 ~ 01111111,真值范围为 -127 ~ 127,可能你发现真值一共只有255 个,因为 10000000 和 00000000 表示的都是 0。
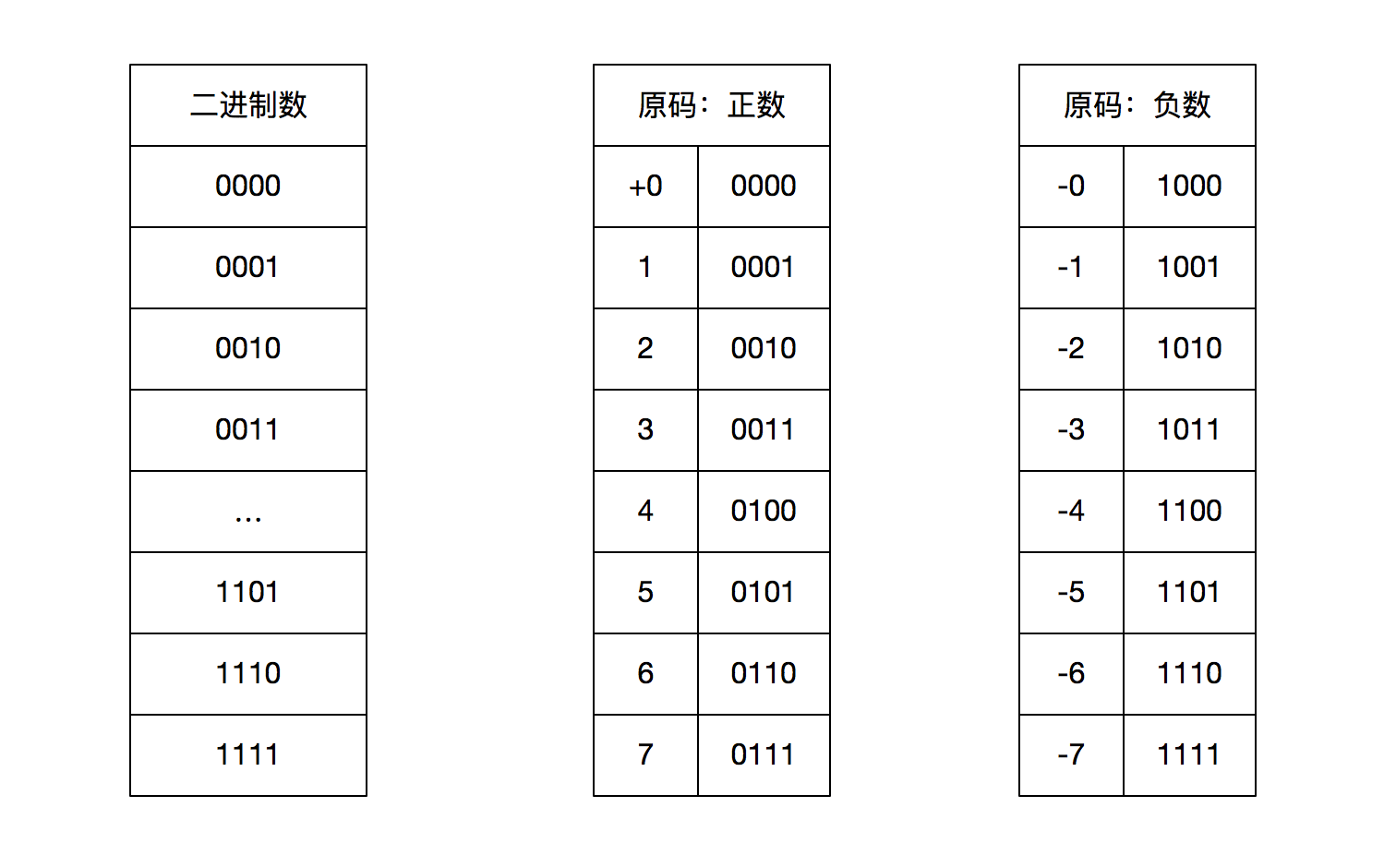
从真值的二进制到原码,我们可以看出,对于机器来说没有区别,只是我们用数学手段赋予了同一个二进制数不同的意义,为的是能够让计算机满足我们的计算需求。跟随这个思想,我们同样也能理解反码和补码。
反码
从真值的二进制到原码,我们跨出了一步,在计算机中引入了负数。但是原码存在很严重的问题,就是对于 -1:10000001和 +1:00000001,他们的和是 10000010,按照原码的约定规则,这个数是 -2,这样显然是不行的,电路也无法设计。对于人类来说,分辨第一位是符号为很简单,我们会根据符号选择对后面的绝对值进行加还是减并得出结果。但是对于计算机来说将符号位分开处理是一件非常复杂的事情,如果我们把基础的加减乘除运算的电路都设计的非常复杂,那么这个计算机的性能显然是很差的。现在的问题是如何让符号位能够参与运算,并且形成一个完善的逻辑。
为了解决这个问题,我们引入了反码,反码的定义是:如果是正数则保持不变,如果是负数,则除符号位之外按位取反。具体看下图。
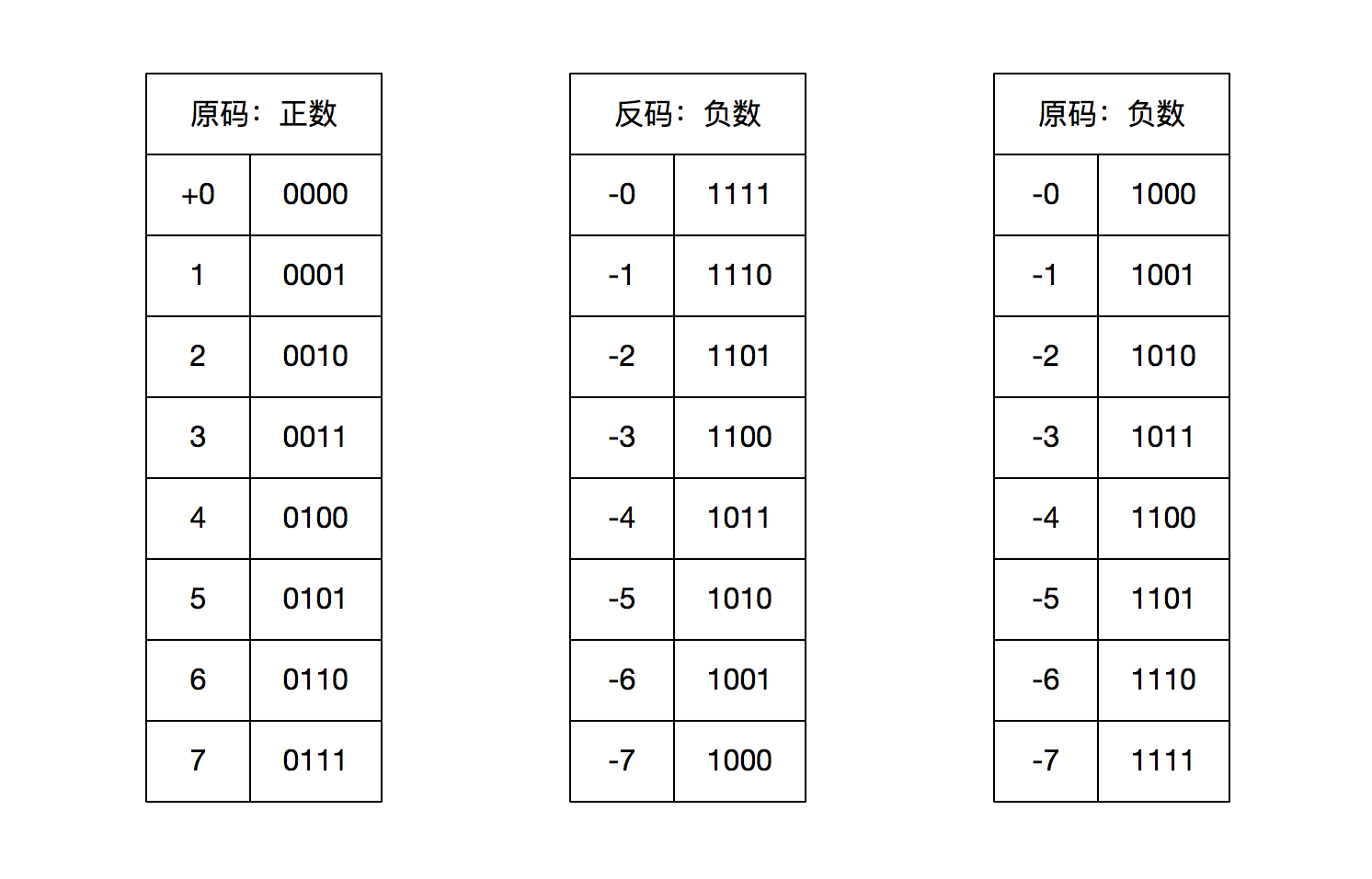
通过反码逻辑的设计,我们可以发现现在正负数相加获得的都是 1111,也就是 -0,现在我们已经可以设计电路然后用计算机进行存储和计算了。
补码
反码解决了带符号位运算的问题,但是还有一个问题没有解决,就是现在我们有两个 0,一个 +0, 一个 -0,这两者在数学上是没有区别的,并且占了两个编码。为了解决这个问题,又引入了补码。
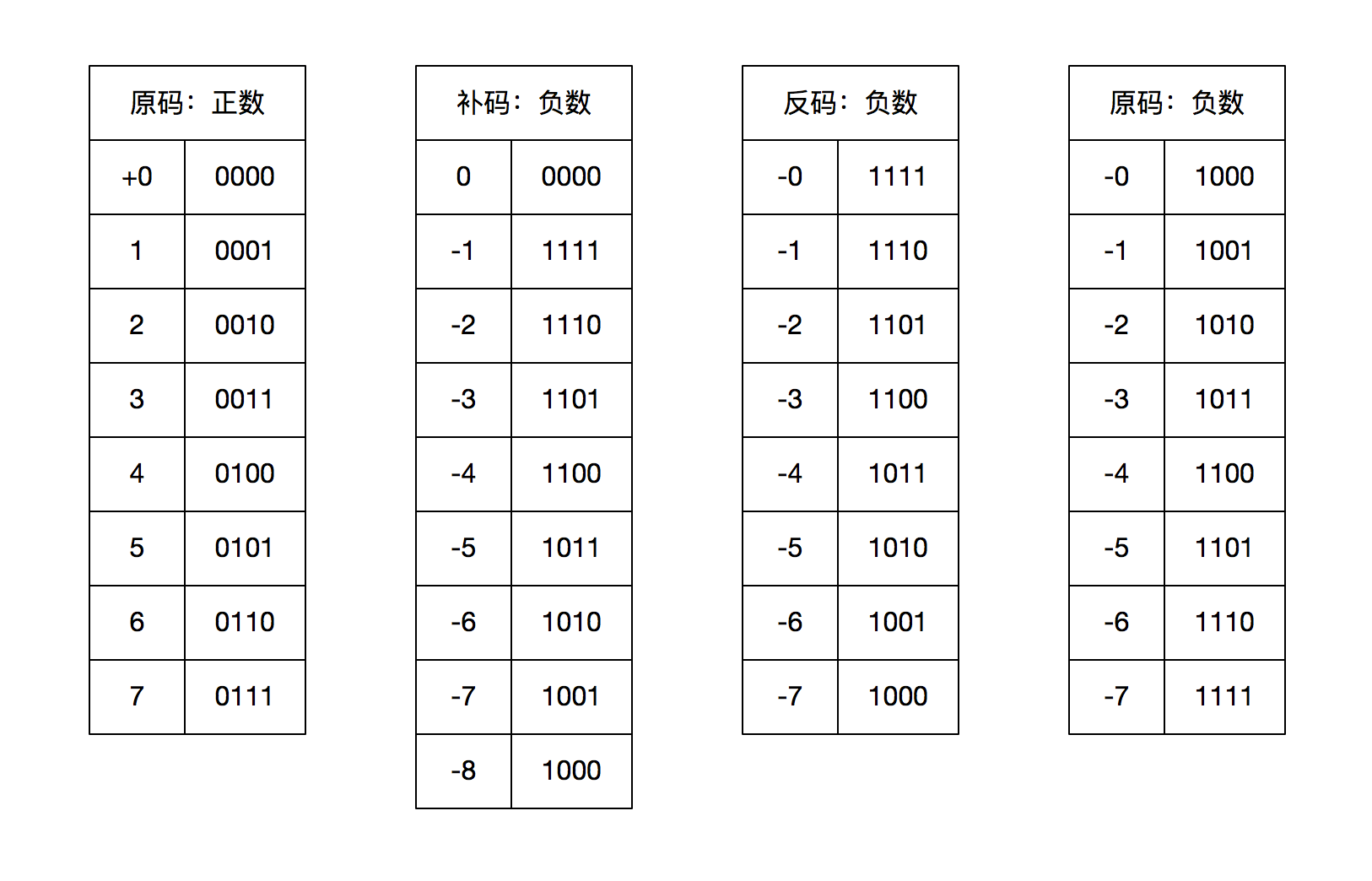
补码的定义就是正数和 0 的补码不变,负数的补码是其对应的正数按位取反再 +1。负数也可以说成是反码 +1。还以 8 为存储单位为例,-1 的原码是 10000001,反码是 11111110,补码在反码的基础上 +1,即为 11111111。
从图中可以看出,-0 取补码后跟 0 是一致的,解决了两个 0 的问题。在 -1 ~ -7 之后,还多处一个编码 1000 可以用来表示 -8,这也就是我们今天计算机所用的存储和计算的方式。
数学原理
其实上面的补码定义肯定让很多人产生疑问,最后这个 -8 到底是哪来的?这是因为这个通用的教科书定义只是给出了补码之形,并没有告诉我们补码之质,表面上是要让我们更好的理解补码,其实更容易让人产生误导。上面的内容一步一步介绍补码,感觉似乎补码是 设计 出来的,但其实只是编码背后存在一定的数学规律,而补码正式最合适的那个,所以被用来实现计算机了。
同余
先来说一说同余概念,我们来看看下面的表盘

表盘上的指针指向 8,那如果我现在要调节指针指向 1 要如何操作呢?
1. 顺时针拨动 5 个小时 (8 + 5) mod 12 = 1
2. 逆时针拨动 7 个小时 (8 -7) mod 12 = 1
对于表盘来说,我们顺时针拨动 5 个小时和逆时针拨动 7 个小时是没有区别的。甚至我们可以顺时针拨动 5 + 12n 个小时,或者逆时针拨动 7 + 12n 个小时。换一个角度,现在指针指向 8 ,如果只看这个表盘你并不能分辨现在是早上 8 点还是晚上 20 点。
从上面的现象我们可以总结出两点结论,
1. 如果把顺时针看作加法,把逆时针看作减法,那么一个闭合的连续自然数环的减法和加法是可以互相替代的。
2. 5 和 5 + 12n 的效果相同,也就是说只要相对于环的数字总数的余数相同,那么效果相同。
这个规律就是数学中的同余:两个整数 a,b,若它们除以整数 m 所得的余数相等,则称 a,b 对于模 m 同余。记作 a ≡ b (mod m),a 与 b 关于模 m 同余。
5 mod 12 = 5
17 mod 12 = 5
29 mod 12 = 5
所以 5,17,29 关于模 12 同余。
同余的数学定义是:
$$ x \bmod y = x\,-\,y\,\llcorner\,x/y\,\lrcorner $$
x mod y 等于 x 减去y 乘上 x 与 y 的商的下界。举个例子 -3 mod 2等于$ -3 – 2 \times \llcorner -1.5\lrcorner $,等于 -3 - 2 * (-2),结果为 1。
同余的深入
介绍完同余的概念,要理解为什么计算机使用补码,我们还需要知道一点:由于计算机的字长是有限的,所以计算机的运算本质就是同余运算,比如字长 32 位,一共能表示 $2^{32}$ 共 4294967296 个状态,当我们计算 1 + 2 的时候,本质是这样的:
a ≡ 1 (mod 4294967296)
b ≡ 2 (mod 4294967296)
r ≡ a + b ≡ 3 (mod 4294967296)
在回到上面的表盘,我们把表盘上的 12 写作 0,现在我们的表盘就表示从 0 ~ 11 一共 12 个数。我们以 0 为起点,12 为模,逆时针拨动指针就得到负数,顺时针拨动指针就是正数。比如我们逆时针拨动一格,我们就得到 -1,-1 和 11 关于模 12 同余,所以他们等价。利用同余的这种性质,我们引入了负数,
那么如果我们把00000000 ~ 11111111 放到一个表盘上呢,它的规律和只有 12 格的表盘是一样的,11111111 可以表示 255 也可以表示 -1,在同余计算中他们是等价的。那么8位 一共 256 个状态,我们既然要引入负数当然希望正数负数一样多,于是我们从 00000001 ~ 01111111 表示 1 ~ 127,11111111 ~ 10000001 表示 -1 ~ -127,还多出两个数 00000000 和 10000000。00000000 自然是表示 0,那么 10000000 表示什么呢?它既可以表示 128 也可以表示 -128,但是为了统一性以方便数据处理,我们用 10000000 来表示 -128,这样所有的负数的最高位都是 1。这些负数的二进制编码就是所谓的补码了。
介绍了半天,告诉大家 -8 到底是哪来的,可以好像又脱离的补码的概念了,补码的本质到底是什么?其实补码只是上面一段内容背后的数学规律,我们用 11111111 ~ 10000000 表示了 -1 ~ -128,那比如我想知道 -57 的二进制码是多少,要怎么计算呢?
在二进制计算中我们很容易可以发现一个规律就是 X + ~X + 1 = 0,~X 表示 X 的反码,我们将这个式子处理一下:-X = ~X +1,是不是很熟悉,我们要求一个负数的二进制表示,只要将其对应的正数的反码 +1 就可以了。
反码和补码的英文
反码的英文是 Ones' complement,这是因为原码加上反码得到的是全为 1 的二进制,所以这个翻译的意思就是原码相对于全 1 的编码的补,也就是字面意思,这里的 Ones' 就是很多一的意思。
补码的英文是 Two's complement,一个 n 位的二进制数,其模为 $2^n$,一个负数 m 的补码即为 $2^n + m$,所以这里的翻译就是相对于模来说的。
总结
补码的本质就是由于计算机字长的限制,让我们在计算机中的数的表示是有限的,形成了一个环,计算的本质也是同余运算。说直白一点,就像钟表上的 12 个点,我们可以认为是 0~11 ,也可以是 1~12 ,甚至可以是 3~14,它们都会遵循同余运算的特点,而我们选择哪一种取决于我们的计算需求。而在计算机中我们选择了对计算机设计最有利的一半负数,一半非负数的表示,并不是人为设计出来的。而在这种情形下的负数的二进制码是不直观的,书本上的补码概念正是阐述负数二进制码的数学规律,方便我们能够计算负数的编码。
可能内容讲的有点乱,写文章的花了很久,不知道如何用更通俗的语言表述,肯能是自己的理解还不够透彻,如果又表述的不清晰或者不对的地方欢迎指正。




1 个评论
core · 2023年1月1日 - 下午2:41